Draw a Box Plot That Represents the Data

In this article, we will try to sympathize the concept behind box plots. When i starting time saw a box plot, I was utterly confused and could not extract much information out of information technology on the showtime go. This article will help y'all to avoid the situation I faced in understanding a box plot.
Introduction to box plots
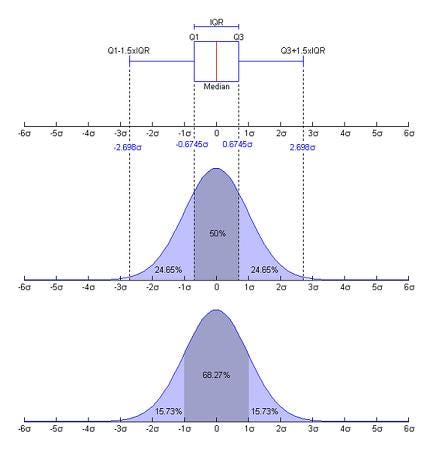
A Box and Whisker Plot (or Box Plot) is a convenient manner of visually displaying the data distribution through their quartiles. It is a graphical rendition of statistical data based on the minimum, first quartile, median, third quartile, and maximum. The term "box plot" comes from the fact that the graph looks like a rectangle with lines extending from the top and lesser. Because of the extending lines, this type of graph is sometimes chosen a box-and-whisker plot.

Permit us understand these 5 components of the box plot
- Median Value
Value or quantity that falls halfway between a set up of values bundled in an ascending or descending social club. When the fix contains an odd number of values, the median value is exactly in centre. If the number of values is even, the median is computed past averaging the 2 numbers closest to the middle. - Lower Quartile(Q1)
The lower quartile is also known as the first quartile, splits the lower 25% of the data. Quartiles are iii points that divide the data fix into iv equal groups. Each group represents the one-fourth of the data ready. The lower quartile is the middle value of the lower half. - Upper Quartile(Q3)
Upper quartile is likewise known every bit the third quartile. It splits lowest 75% (or highest 25%) of data. It tin exist also seen as the center value of the upper one-half. - Interquartile Range(Q3-Q1)
The Interquartile range is from Q1 to Q3. Information technology is the departure between the lower quartile and upper quartile. The IQR is oft seen as a better mensurate of a spread than the range (highest value-lowest value) as it is not affected by outliers. - Highest Value
This point in the box plot represents the highest value in the data distribution over which the box plot is built which is not an outlier. This point does not correspond to the highest value in your dataset. Suppose you have some data similar 65,76,87,100,105,100000. Hither the largest value is 100000 only information technology is most likely to exist an outlier and hence the box plot will not mark this as the maximum value. The most feasible option will be 105 every bit the maximum value of the box plot. - Everyman Value
This point in the box plot represents the lowest value in the information distribution over which the box plot is built and is non an outlier (smallest value in the Interquartile range of the distribution). This point does not correspond to the smallest value in your dataset. Suppose you take some data like 0.005,65,76,87,100,105. Hither the smallest value is 0.005 merely information technology is nearly likely to exist an outlier and hence the box plot will not marking this equally the minimum value. The most viable selection will be 65 as the minimum value of the box plot.
Why box plots?
- Handles Large Information Easily
Due to the 5-number data summary, a box plot can handle and present a summary of a big amount of data. A box plot consists of the median, which is the midpoint of the range of information; the upper and lower quartiles, which represent the numbers above and below the highest and lower quarters of the information and the minimum and maximum data values. Organizing data in a box plot by using five key concepts is an efficient way of dealing with large data too unmanageable for other graphs, such equally line plots or stem and foliage plots. - Exact Values Not Retained
The box plot does non keep the exact values and details of the distribution results, which is an issue with handling such big amounts of data in this graph blazon. A box plot shows but a unproblematic summary of the distribution of results so that y'all can apace view it and compare it with other data. Apply a box plot incombination with another statistical graph method, like ahistogram, for a more thorough, more detailed analysis of the information. - A clear summary
A box plot is a highly visually effective style of viewing a clear summary of one or more sets of data. It is particularly useful for quickly summarizing and comparing different sets of results from different experiments. At a glance, a box plot allows a graphical display of the distribution of results and provides indications of symmetry within the data. - Displays outliers
A box plot is one of very few statistical graph methods that testify outliers. At that place might be one outlier or multiple outliers within a ready of information, which occurs both beneath and higher up the minimum and maximum data values. By extending the lesser and greater data values to a max of 1.5 times the inter-quartile range, the box plot delivers outliers or obscure results. Whatsoever results of data that autumn exterior of the minimum and maximum values known as outliers are easy to determine on a box plot graph.
Understanding different box plots
We have data on different firm prices in 5 different areas of Bangalore. Nosotros will try to empathize the distribution of this data and attempt to find some insights out of information technology.

The Box plot every bit an Indicator of Axis
We will endeavour to gather our commencement insight by observing the centrality of the box plots. Centerline represents the median value for the house price in different areas. Houses on airport route have the highest median value of the business firm which makes information technology a comparatively expensive place to live in whereas houses in Marathali have the least median value which allows the states to conclude that houses hither are relatively cheapest to live.
The Box plot as an indicator of the spread
The spread of a box plot talks well-nigh the variance nowadays in the information. More the spread, more the variance. If you look closely at the starting time two box plots, both Whitefield and Hoskote areas accept the aforementioned median business firm price value then it seems like both places autumn into the same upkeep category. But if we look more than closely, we tin discover that width of Hoskote box plot is more than Whitefield box plot. Hoskote area has more variance in house price as compared to Whitefield i.e. Hoskote offers more multifariousness of budget in houses as compared to Whitefield. If we look at the overall graph, we observe that Bellathur surface area has the most spread in its box plot. This clearly states that this area has the widest diversity in the budget of the houses.
The Box plot as an indicator of symmetry
Symmetry around the median talks about skewness nowadays in the data. If the median line is towards the lower one-half of the box plot, so it is right skewed (positive skew) and if the median line is towards the upper portion of the box plot then it is left-skewed (negative skew). If we expect at the box plot representing Marathalli, we can detect that median is towards the lower half of the box plot and hence it is right skewed (positive skew) which ways that near of the houses are on the cheaper side in Marathalli and only a few are expensive.
The Box plot every bit an indicator of tail length
Tail length talks about the kurtosis present in information. There are 3 cases hither. Either your data will exist unremarkably distributed or it volition have more than data in its tail equally compared to a normal distribution(platykurtic) or it will have fewer information in tails every bit compared to a normal distribution(leptokuritc). A long tail shows that the distribution is platykurtic and shorter tail gives the idea of distribution beingness leptokurtic. In above example, Marathalli has the shortest tail as compared to other box plots which may mean that in Marathalli most of the house prices lie in the interquartile range (q3-q1).
Types of box plots
Variable width box plots
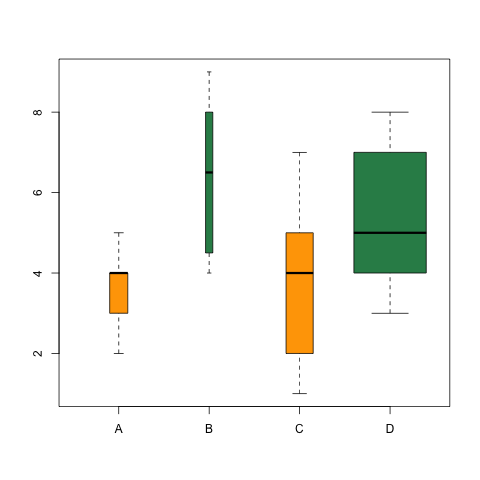
Box plot represents a numeric vector of data that is divide in several groups. When the number of points in each group is highly unlike, it can exist great to represent it using the width of the box. The widths of the box plot indicate the size of the samples. The wider the box, the larger the sample. This is usually an option in statistical software programs, not all Box Plots accept the widths proportional to the sample size. One common convention is to brand the width of the boxes for a group of data proportional to the square roots of the number of observations in a given sample.
Notched box plots
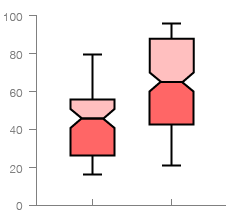
Information technology works the same as a standard Box Plot, just has a narrowing of the box around the median value. This acts as a handy visual guide to help read and compare the differences between the median values across each data series. Notches visually illustrate an judge on whether in that location is asignificant difference of medians. The width of the notches is proportional to the inter quartile range of the sample.
Complications in box plots
- Box plots generally do not go well when the sample size of distribution is pocket-size.
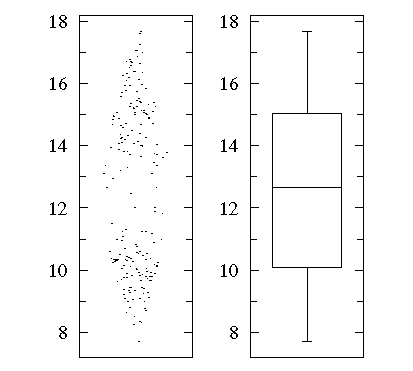
- One case of particular concern — where a box plot can be deceptive — is when the data are distributed into "ii lumps" rather than the "i lump" cases we've considered so far. A "bee swarm" plot shows that in this dataset there are lots of data nearly 10 and fifteen only relatively few in between. Encounter that a box plot would not give yous whatever evidence of this.
Source: https://dimensionless.in/what-is-a-box-plot/